Computer-assisted equilibrium validation for the diblock copolymer model
- Thomas Wanner:
Computer-assisted equilibrium validation for the diblock copolymer model
Discrete and Continuous Dynamical Systems, Series A 37(2), pp. 1075-1107, 2017.
Abstract
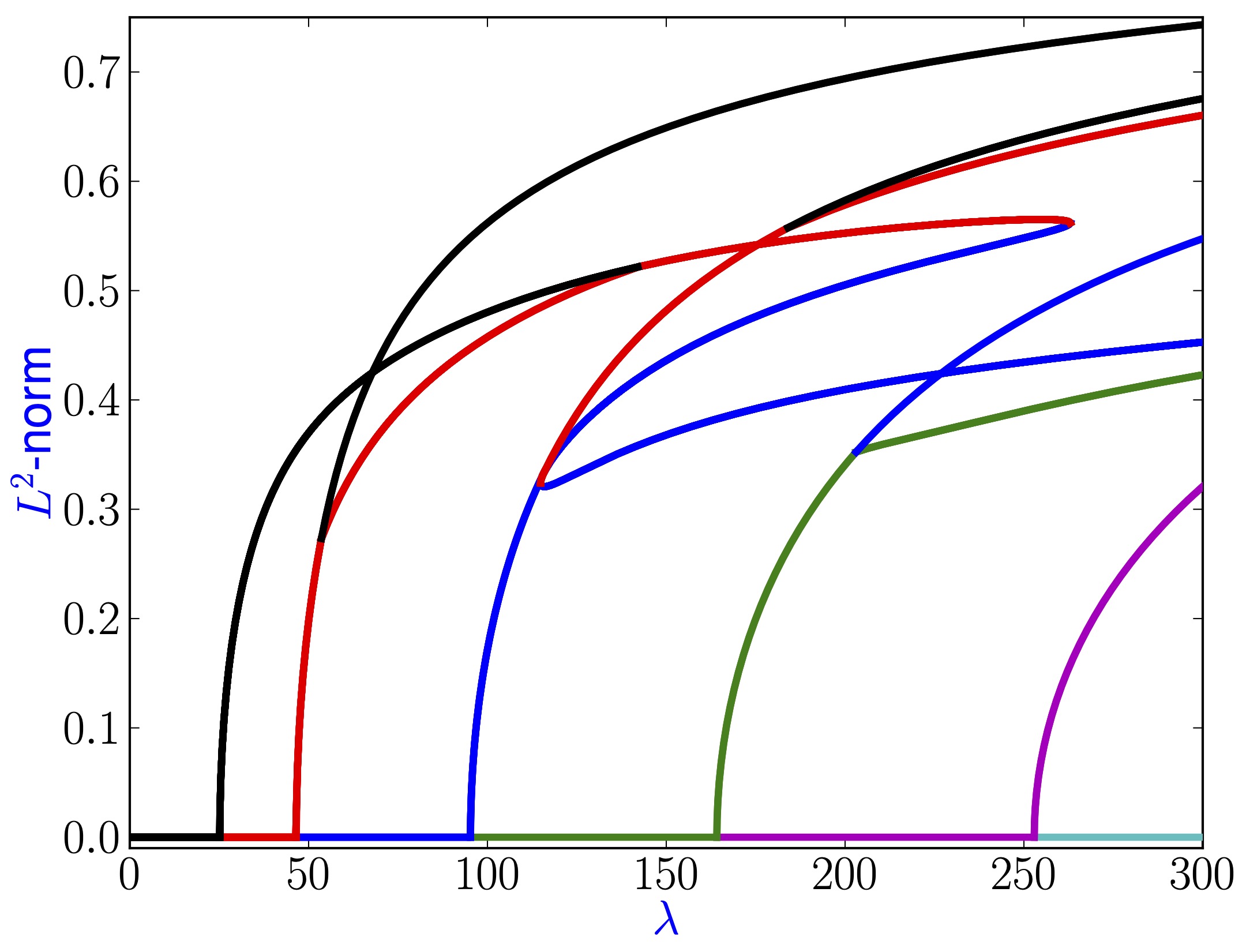
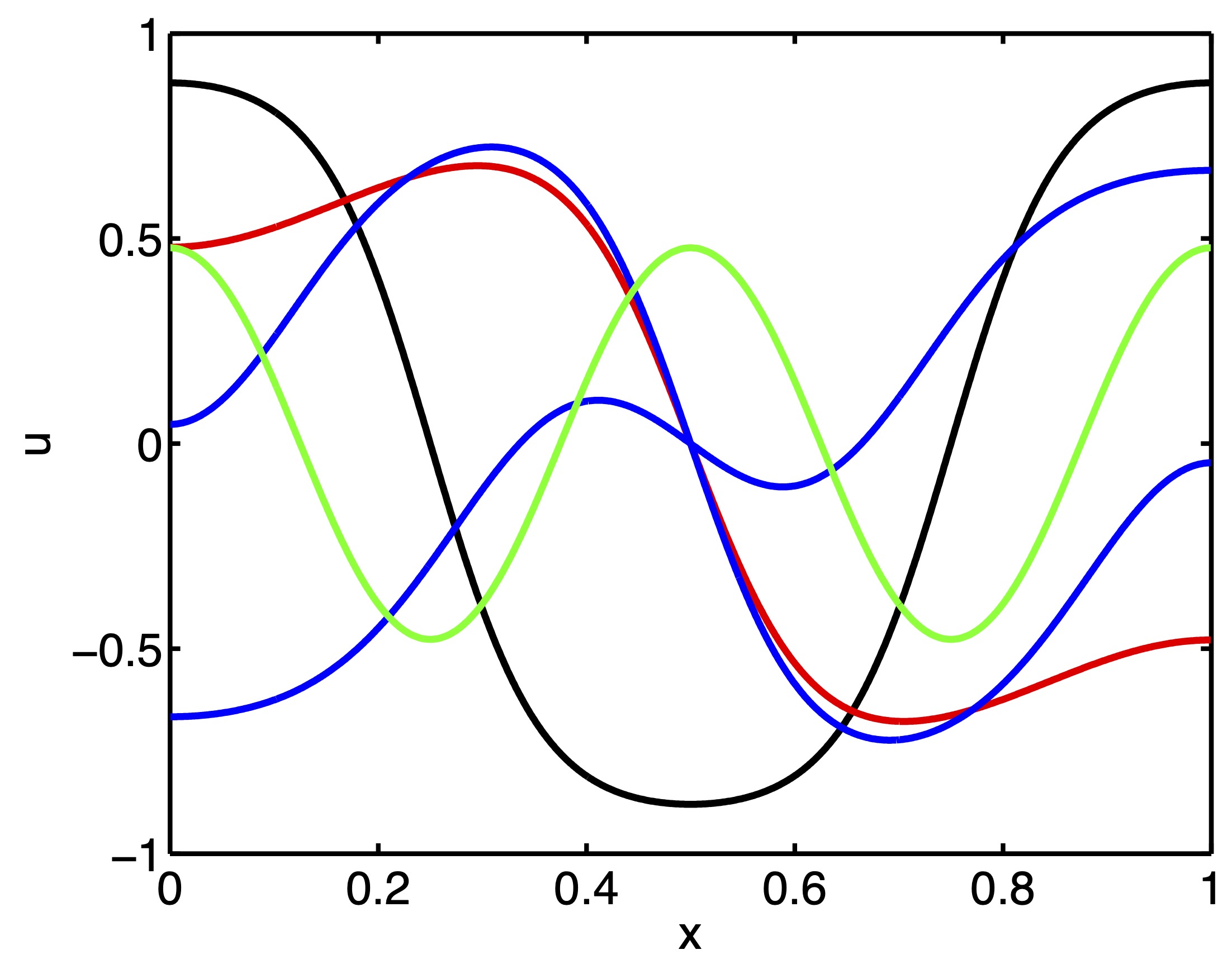
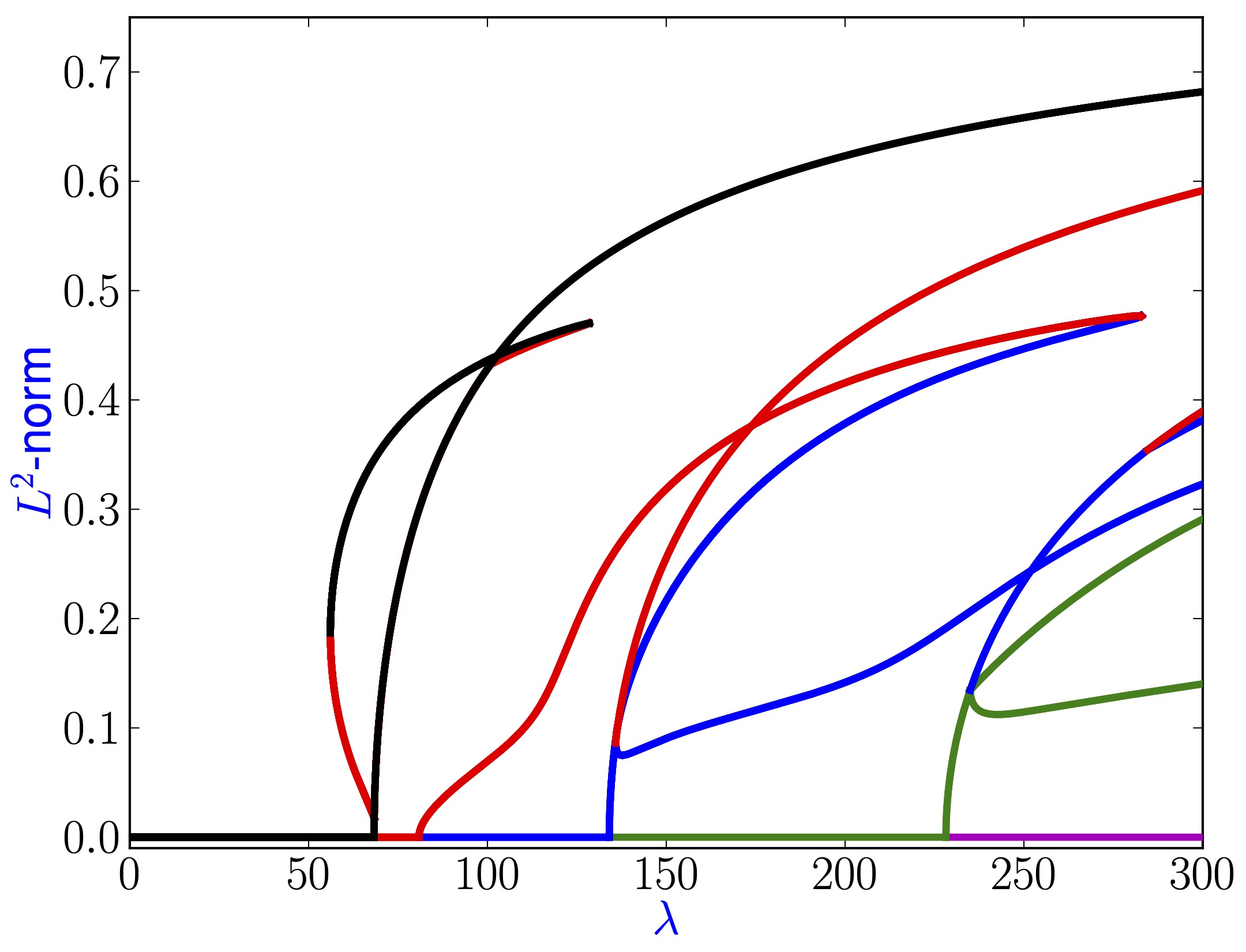
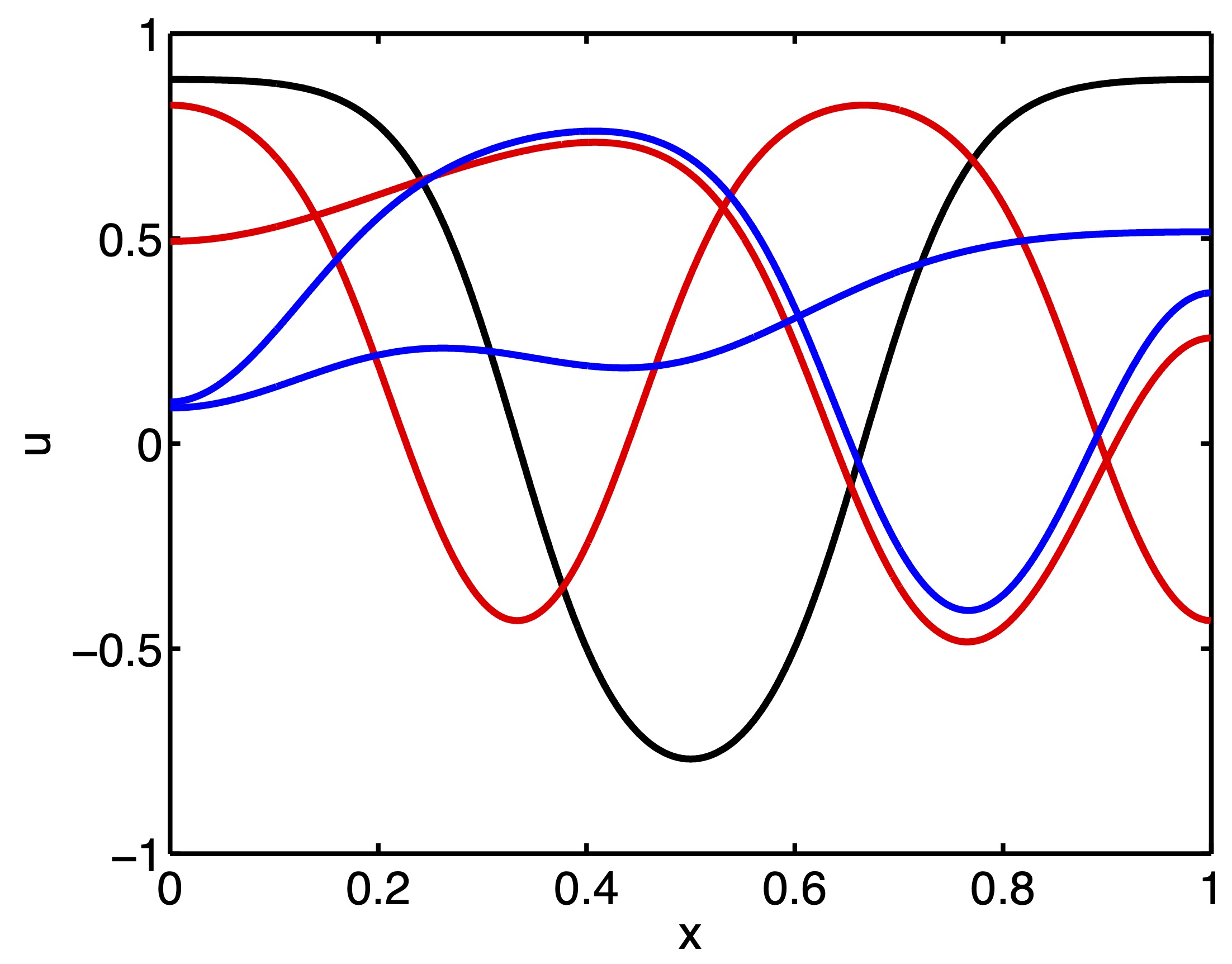
The diblock copolymer model is a fourth-order parabolic partial differential equation which models phase separation with fine structure. The equation is a gradient flow with respect to an extension of the standard van der Waals free energy functional which involves nonlocal interactions. Thus, the long-term dynamical behavior of the diblock copolymer model is described by its finite-dimensional attractor. However, even on one-dimensional domains, the full structure of the underlying equilibrium set is not fully understood. In this paper, we develop a rigorous computational approach for establishing the existence of equilibrium solutions of the diblock copolymer model. We consider both individual solutions, as well as pieces of solution branches in a parameter-dependent situation. The results are presented for the case of one-dimensional domains, and can easily be implemented using standard interval arithmetic packages.
Links
The published version of the paper can be found at https://doi.org/10.3934/dcds.2017045.
Bibtex
@article{wanner:17a,
author = {Thomas Wanner},
title = {Computer-assisted equilibrium validation for the
diblock copolymer model},
journal = {Discrete and Continuous Dynamical Systems, Series A},
volume = {37},
number = {2},
year = {2017},
pages = {1075--1107},
doi = {10.3934/dcds.2017045}
}

 https://orcid.org/0000-0003-3294-0366
https://orcid.org/0000-0003-3294-0366