Spinodal decomposition for the Cahn-Hilliard equation in higher dimensions: Nonlinear dynamics
- Stanislaus Maier-Paape, Thomas Wanner:
Spinodal decomposition for the Cahn-Hilliard equation in higher dimensions: Nonlinear dynamics
Archive for Rational Mechanics and Analysis 151(3), pp. 187-219, 2000.
Abstract
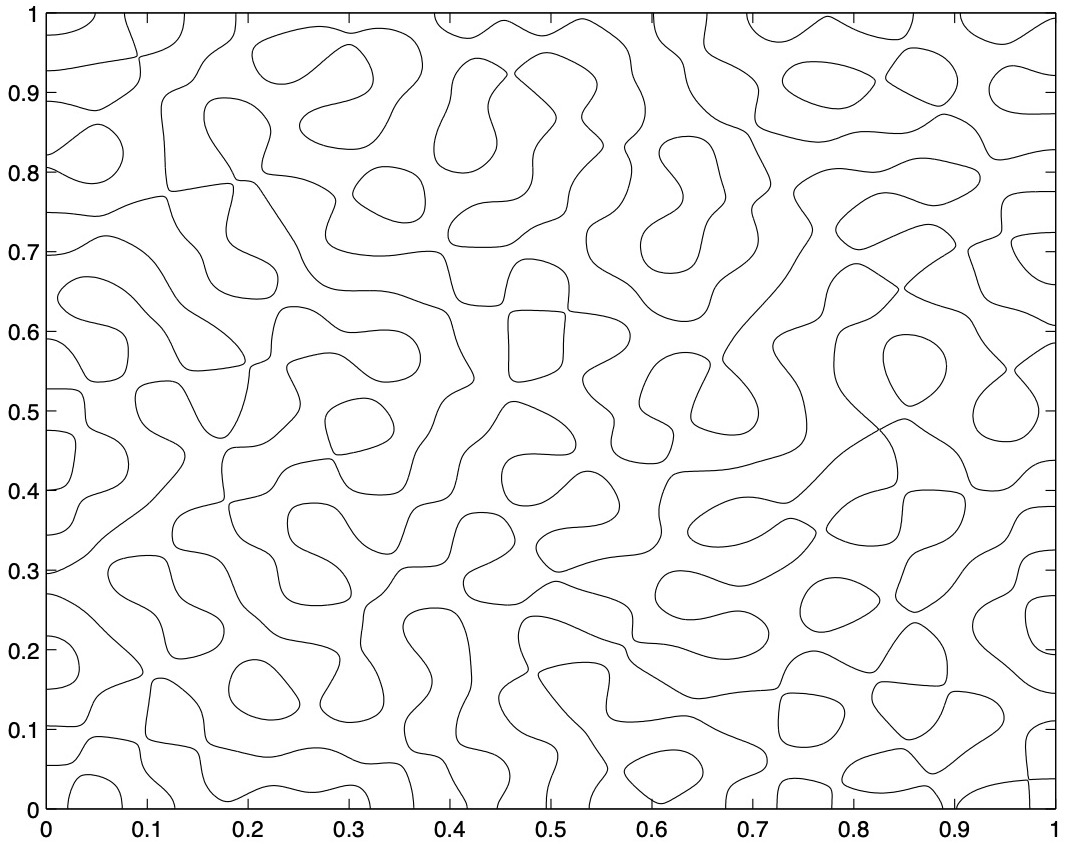
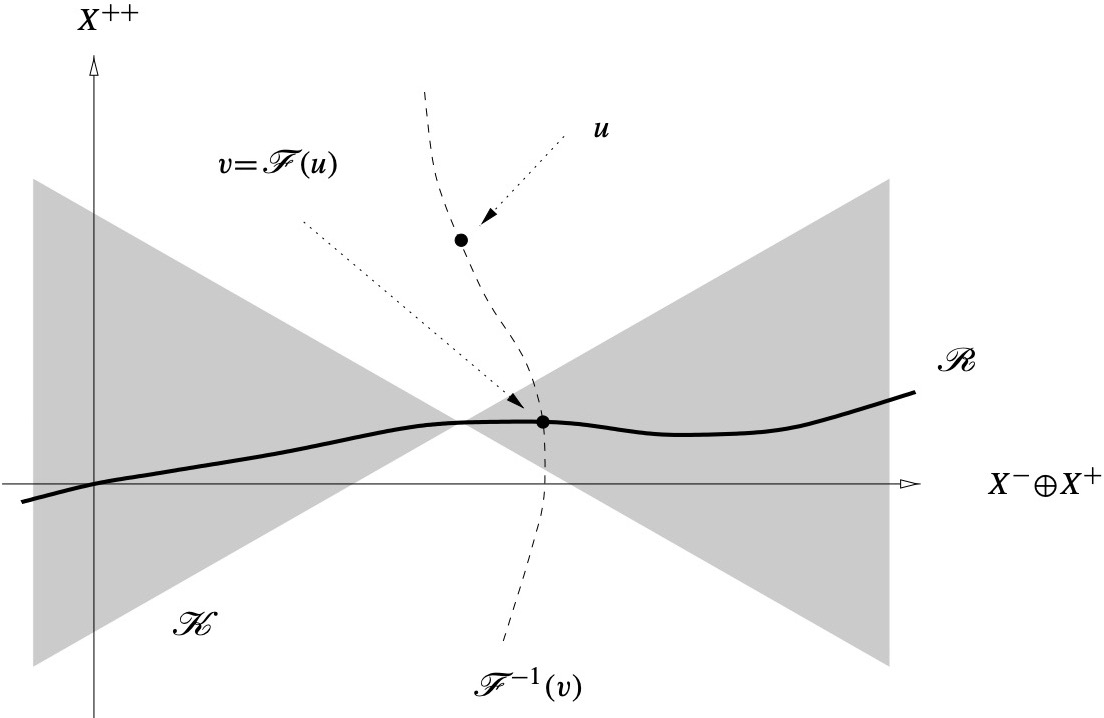
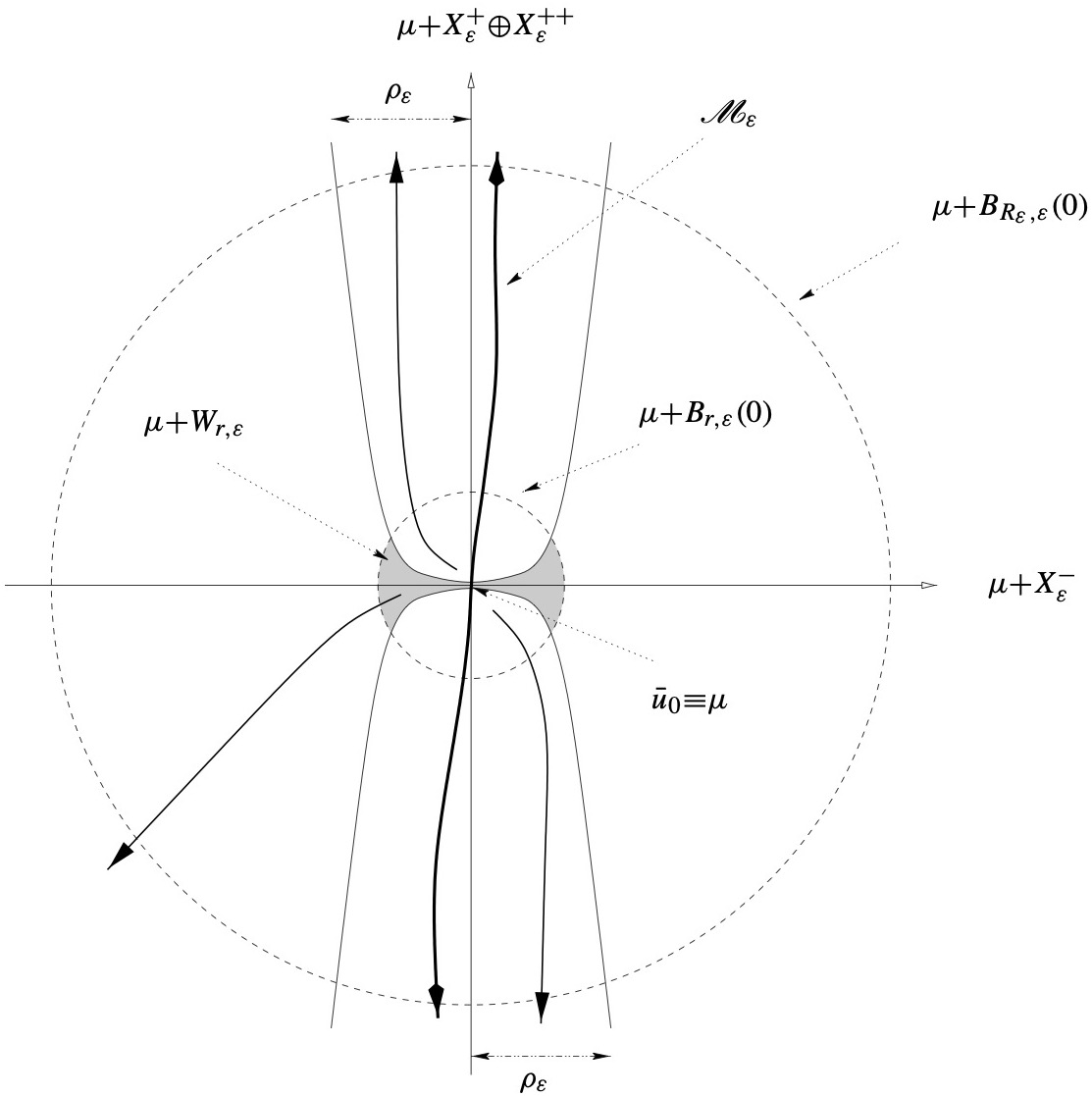
This paper addresses the phenomenon of spinodal decomposition for the Cahn-Hilliard equation $u_t = -\Delta(\epsilon^2 \Delta u + f(u))$ in $\Omega$, subject to $\frac{\partial u}{\partial \nu} = \frac{\partial \Delta u}{\partial \nu} = 0$ on $\partial \Omega$, where $\Omega \subset \mathbb{R}^n$, $n = 1,2,3$, is a bounded domain with sufficiently smooth boundary, and $f$ is cubic-like, for example $f(u) = u - u^3$. Based on the results of Maier-Paape, Wanner (1998) the nonlinear Cahn-Hilliard equation will be discussed. This equation generates a nonlinear semiflow in certain affine subspaces of $H^2(\Omega)$. In a neighborhood $U_{\epsilon}$ with size proportional to $\epsilon^n$ around the constant solution $\mu$, where $\mu$ lies in the spinodal region, we observe the following behavior. Within a local inertial manifold $N_\epsilon$ containing $\mu$ there exists a finite-dimensional invariant manifold $M_\epsilon$ which dominates the behavior of all solutions starting with initial conditions from a small ball around $\mu$ with probability almost $1$. The dimension of $M_\epsilon$ is proportional to $\epsilon^{-n}$ and the elements of $M_\epsilon$ exhibit a common geometric quantity which is strongly related to a characteristic wavelength $\ell$ proportional to $\epsilon$.
Links
The published version of the paper can be found at https://doi.org/10.1007/s002050050196.
Bibtex
@article{maier:wanner:00a,
author = {Stanislaus Maier-Paape and Thomas Wanner},
title = {Spinodal decomposition for the {C}ahn-{H}illiard equation in
higher dimensions: {N}onlinear dynamics},
journal = {Archive for Rational Mechanics and Analysis},
year = 2000,
volume = 151,
number = 3,
pages = {187--219},
doi = {10.1007/s002050050196}
}

 https://orcid.org/0000-0003-3294-0366
https://orcid.org/0000-0003-3294-0366