Solutions of nonlinear planar elliptic problems with triangle symmetry
- Stanislaus Maier-Paape, Thomas Wanner:
Solutions of nonlinear planar elliptic problems with triangle symmetry
Journal of Differential Equations 136(1), pp. 1-34, 1997.
Abstract
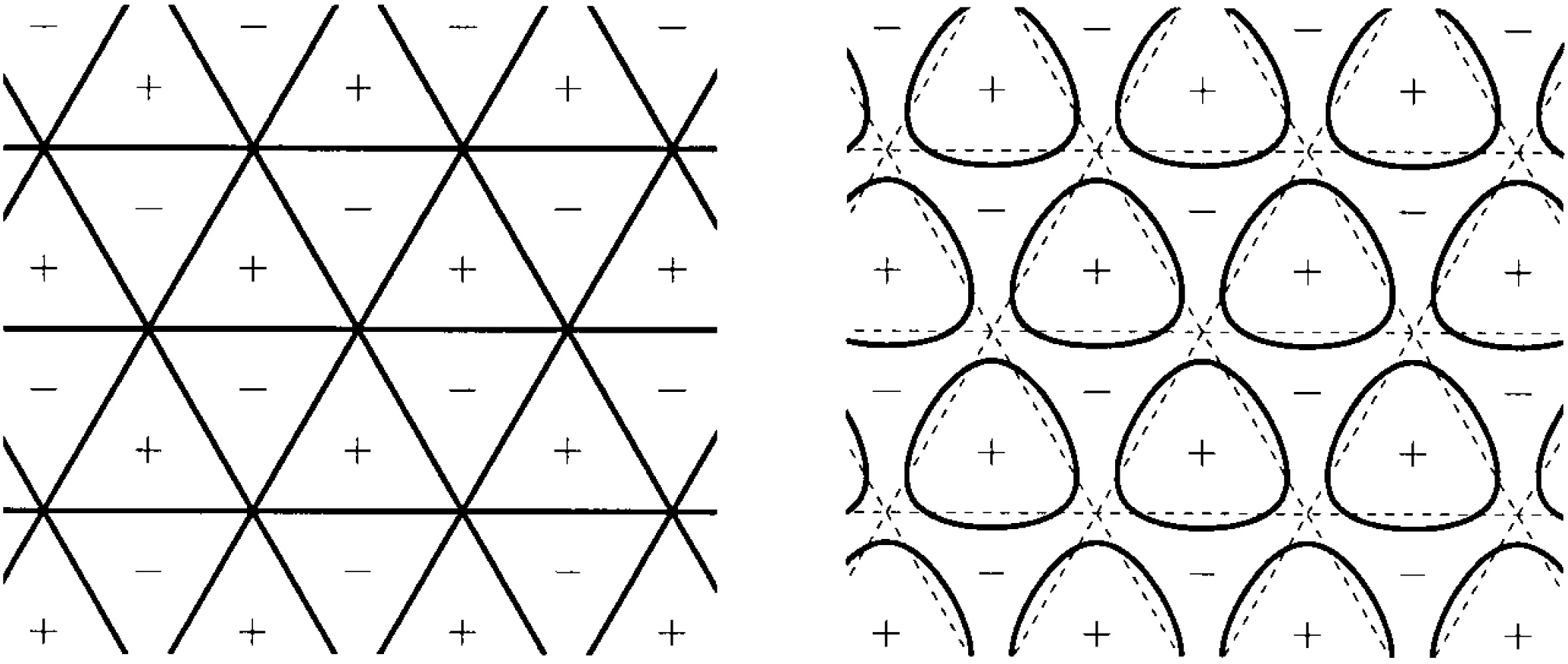
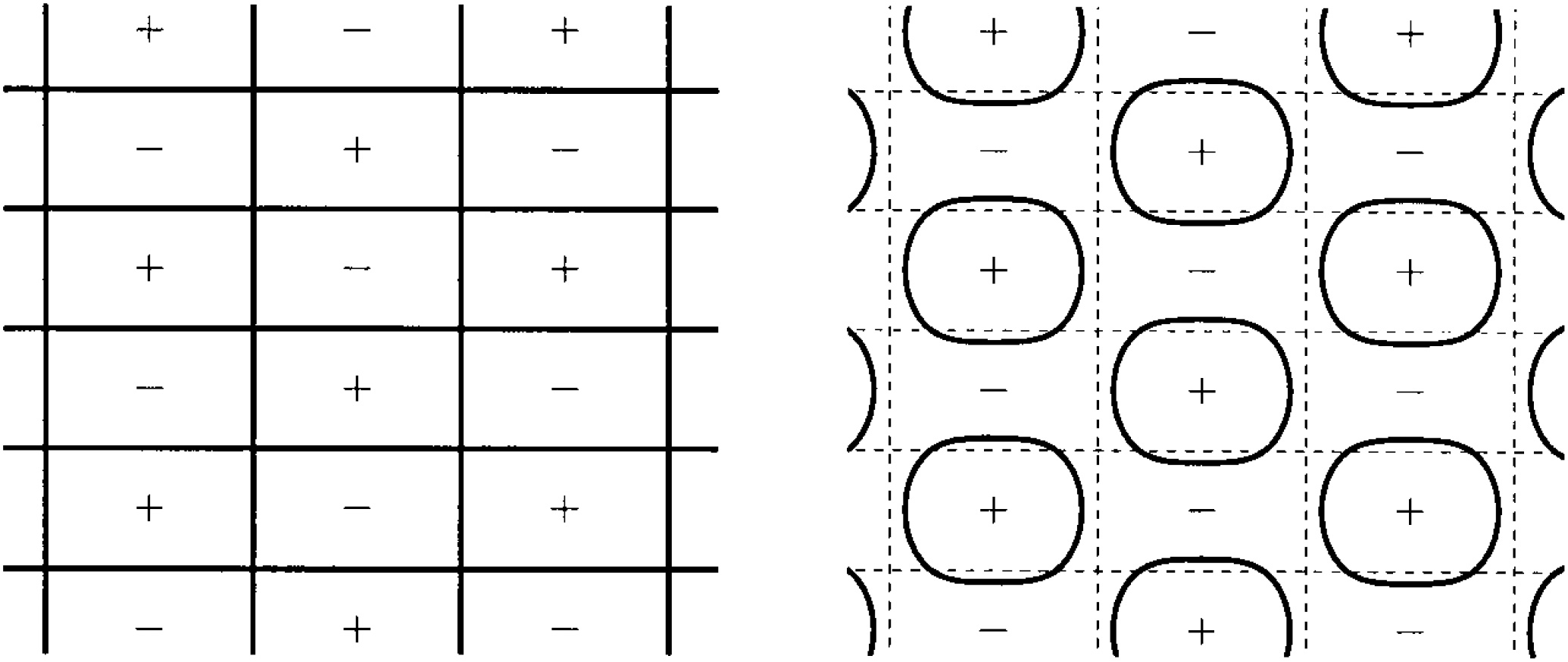
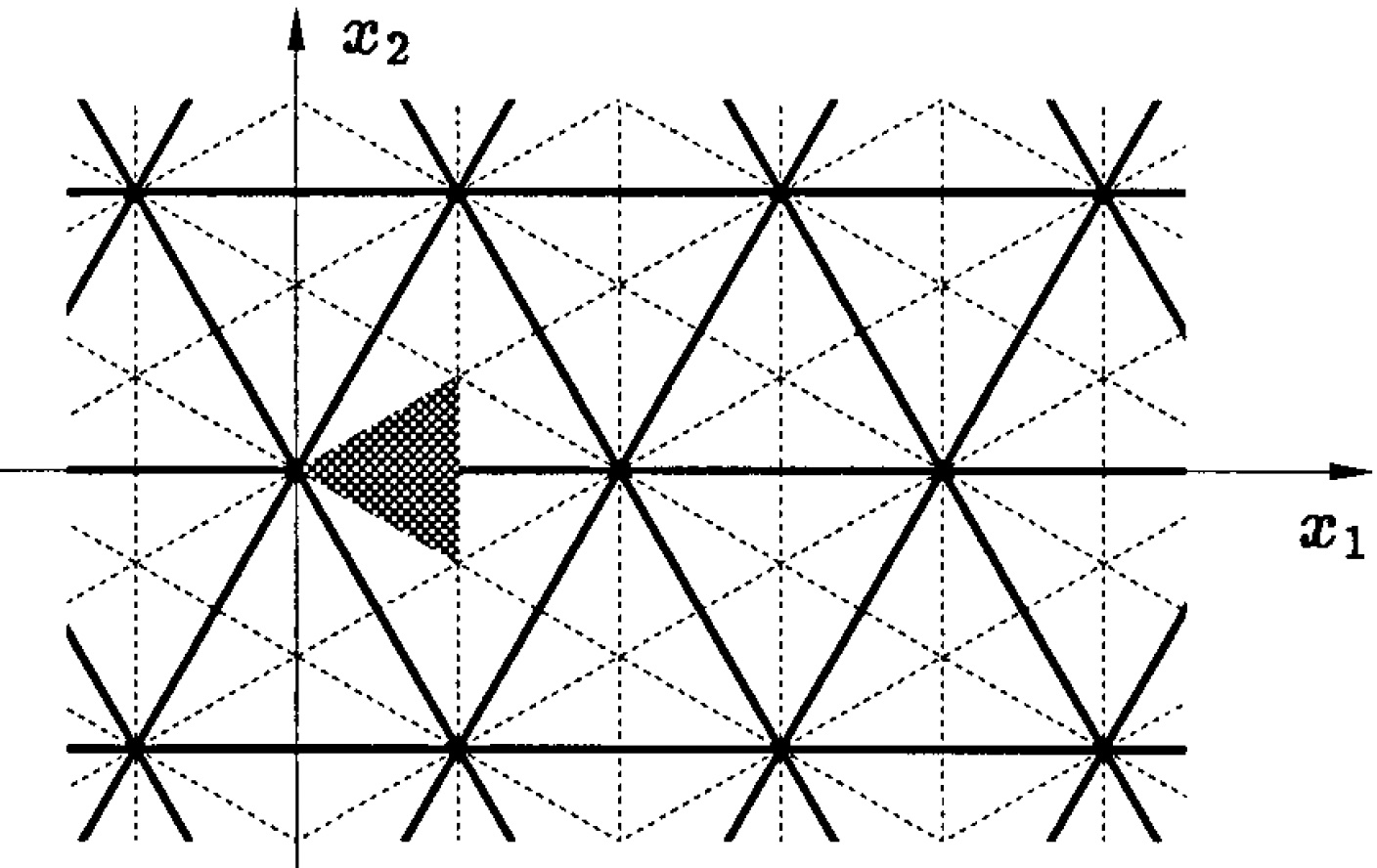
In this paper we continue the study of the nodal domain structure of doubly periodic solutions of certain nonlinear elliptic problems initiated in Fife, Kielhöfer, Maier-Paape, Wanner (1997). More precisely, we consider small amplitude solutions of $\Delta u + \lambda f(u) = 0$ in $\mathbb{R}^2$ whose nodal domains consist of equilateral triangles tiling the plane. If this equation is suitably perturbed, then for generic $f$ we prove the existence of unique nearby solutions with triangle symmetry and show how their nodal domain geometry breaks up. Furthermore, we treat the non-generic rectangular cases which had to be excluded in Fife, Kielhöfer, Maier-Paape, Wanner (1997), as well as other nodal domain structures.
Links
The published version of the paper can be found at https://doi.org/10.1006/jdeq.1996.3240.
Bibtex
@article{maier:wanner:97a,
author = {Stanislaus Maier-Paape and Thomas Wanner},
title = {Solutions of nonlinear planar elliptic problems with
triangle symmetry},
journal = {Journal of Differential Equations},
year = 1997,
volume = 136,
number = 1,
pages = {1--34},
doi = {10.1006/jdeq.1996.3240}
}

 https://orcid.org/0000-0003-3294-0366
https://orcid.org/0000-0003-3294-0366