Perturbation of doubly periodic solution branches with applications to the Cahn-Hilliard equation
- Paul C. Fife, Hansjörg Kielhöfer, Stanislaus Maier-Paape, Thomas Wanner:
Perturbation of doubly periodic solution branches with applications to the Cahn-Hilliard equation
Physica D: Nonlinear Phenomena 100(3-4), pp. 257-278, 1997.
Abstract
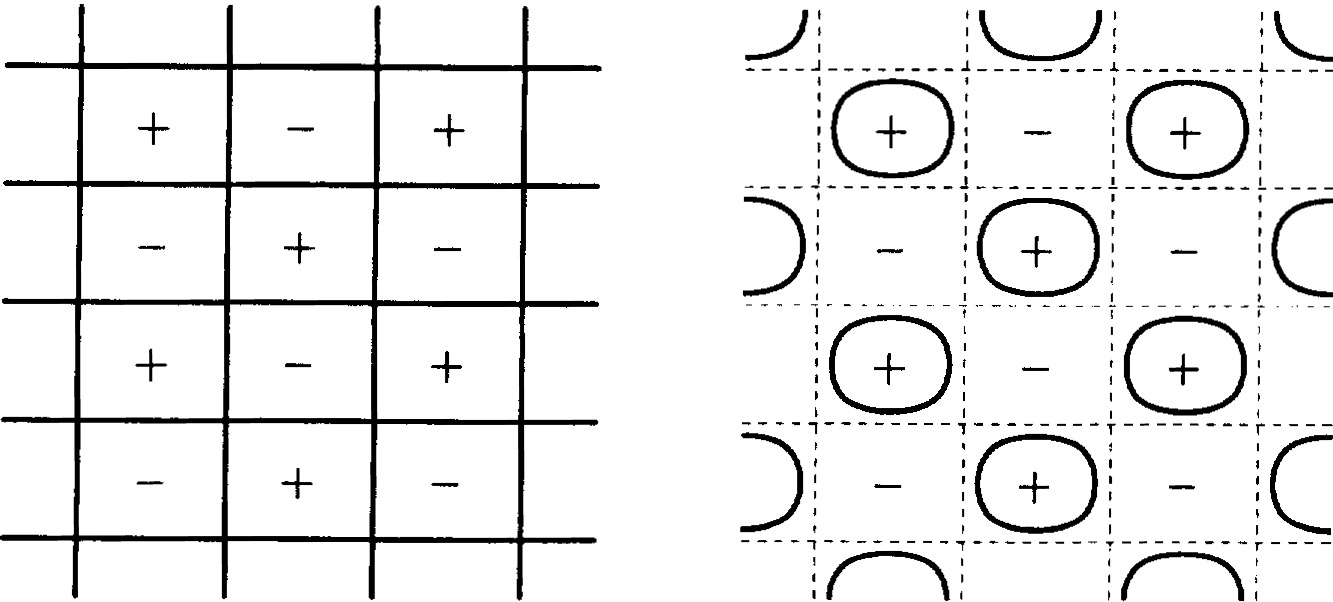
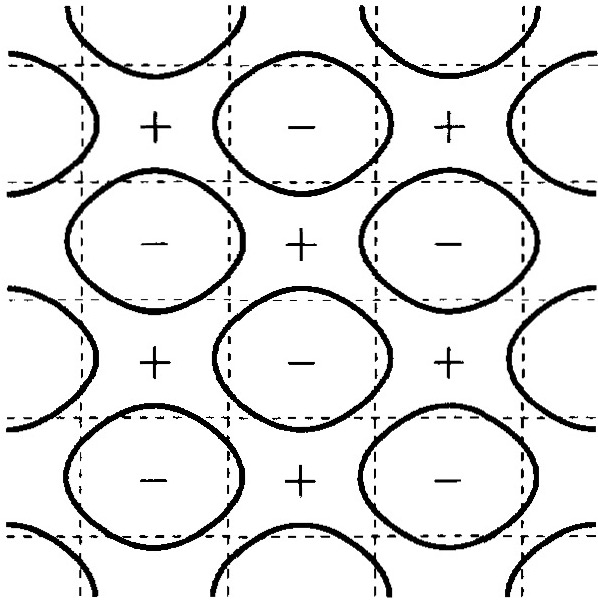
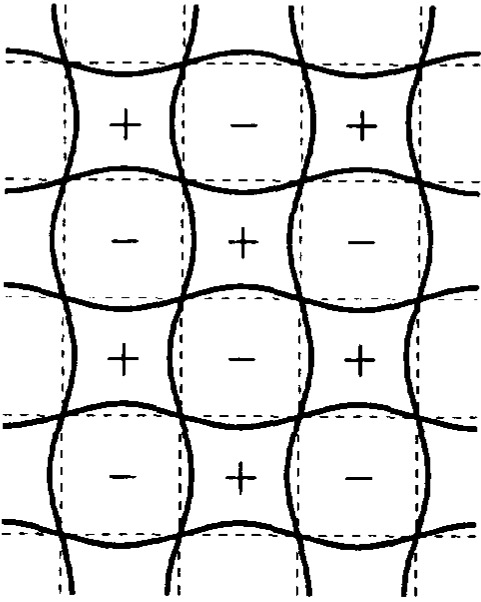
In this paper we prove the existence of doubly periodic solutions of certain nonlinear elliptic problems on $\mathbb{R}^2$ and study the geometry of their nodal domains. In particular, we will show that if we perturb a nonlinear elliptic equation exhibiting a small amplitude doubly periodic solution whose nodal domains form a checkerboard pattern, then the perturbed equation will have a unique nearby solution which is still doubly periodic, but for which the nodal line structure breaks up. Moreover, we indicate what can happen if we start with a large amplitude doubly periodic solution whose nodal domains form a checkerboard pattern, and we relate these solutions to the Cahn-Hilliard equation and spinodal decomposition.
Links
The published version of the paper can be found at https://doi.org/10.1016/S0167-2789(96)00190-X.
Bibtex
@article{fife:kielhofer:etal:97a,
author = {Paul C. Fife and Hansj\"org Kielh\"ofer and
Stanislaus Maier-Paape and Thomas Wanner},
title = {Perturbation of doubly periodic solution branches with
applications to the {C}ahn-{H}illiard equation},
journal = {Physica D: Nonlinear Phenomena},
year = 1997,
volume = 100,
number = {3--4},
pages = {257--278},
doi = {10.1016/S0167-2789(96)00190-X}
}

 https://orcid.org/0000-0003-3294-0366
https://orcid.org/0000-0003-3294-0366