Integral manifolds for Caratheodory type differential equations in Banach spaces

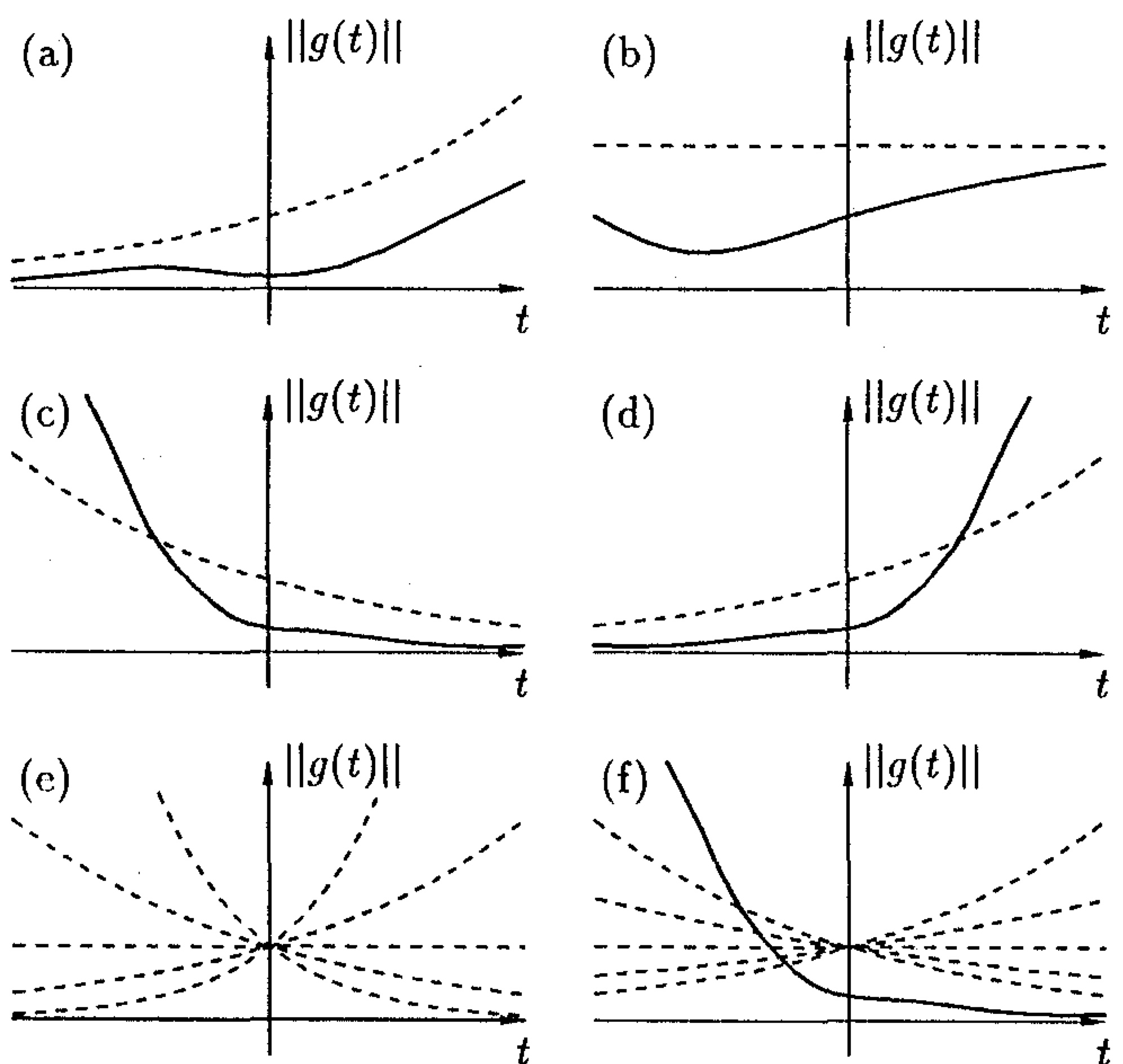
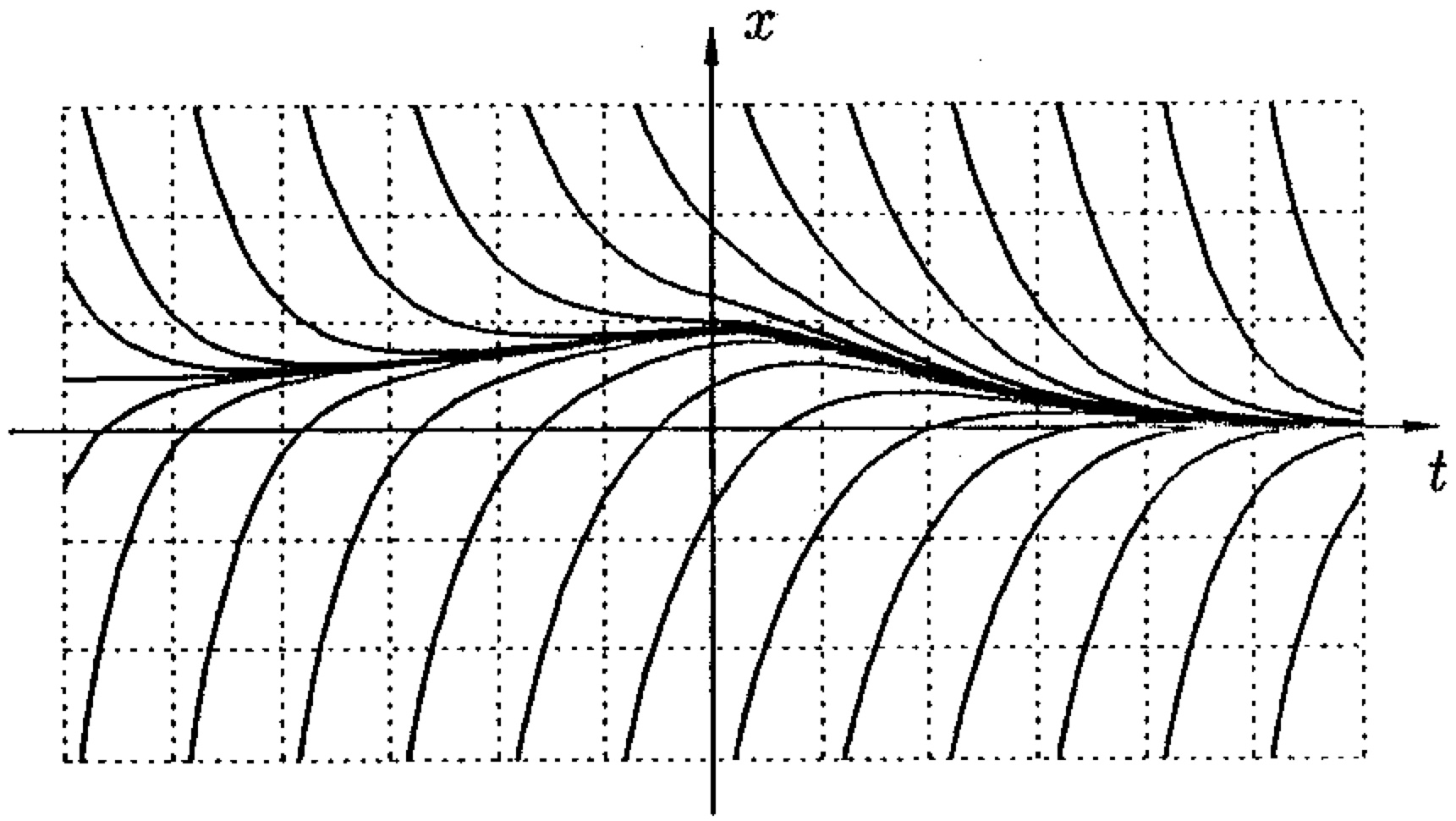
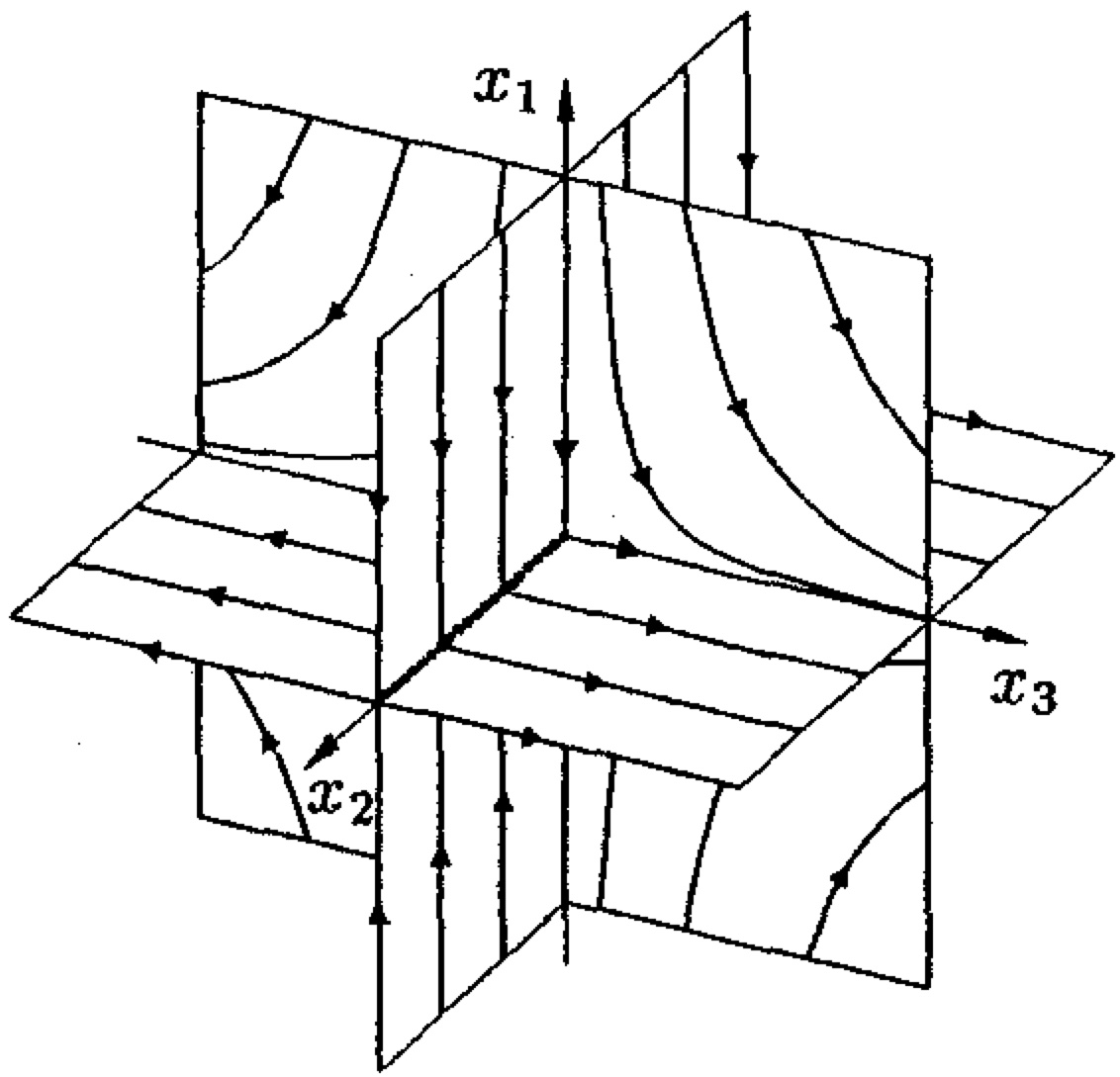
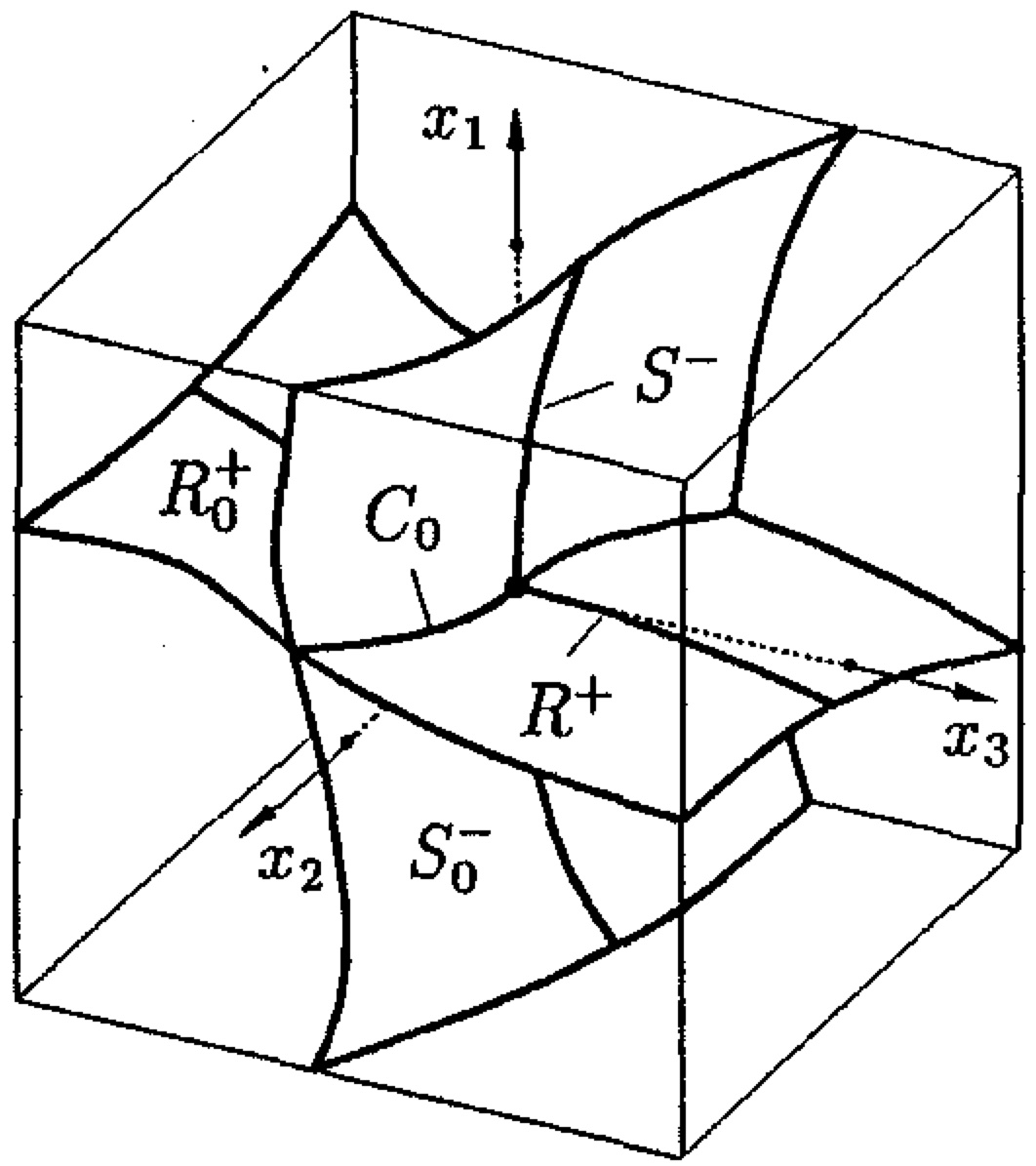
Bernd Aulbach, Thomas Wanner:
Integral manifolds for Caratheodory type differential equations in Banach spaces
In: Six Lectures on Dynamical Systems, edited by Bernd Aulbach, Fritz Colonius, pp. 45-119, World Scientific, Singapore, 1996.

Abstract

This lecture is designed to meet two seemingly contrary purposes. On one hand it is believed to enable a novice to approach the theory of invariant and integral manifolds through a completely selfcontained presentation, and on the other hand it is thought that even the experts may gain some new insight into the theory of integral manifolds, mainly due to a new approach allowing a generalization of the local invariant manifold theory to nonautonomous differential equations $\dot x = f(t,x)$ in Banach spaces with possibly discontinuous t-dependence.

Links

The published version of the paper can be found at https://doi.org/10.1142/9789812812865_0002. It is a chapter of the book Six Lectures on Dynamical Systems, which is available at https://doi.org/10.1142/3012.

Bibtex

@incollection{aulbach:wanner:96a,
   author = {Bernd Aulbach and Thomas Wanner},
   title = {Integral manifolds for {C}arath\'eodory type differential
            equations in {B}anach spaces},
   booktitle = {Six Lectures on Dynamical Systems},
   publisher = {World Scientific},
   year = 1996,
   editor = {Bernd Aulbach and Fritz Colonius},
   pages = {45--119},
   address = {Singapore},
   doi = {10.1142/9789812812865_0002}
   }